12. 循环神经网络(第二部分)
16 循环神经网络 B V4 最后一节
正如我们所见,在前馈神经网络中任何时间t的输出,是当前输入和权重的函数。这可以用以下方程式很容易表示:
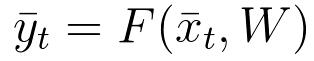
方程式28
在循环神经网络中,我们在时间t的输出不仅取决于当前的输入和权重,还取决于之前的输入。在这个例子中,时间t的输出定义为:
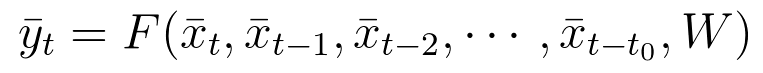
方程式29
这是循环神经网络的折叠模型:
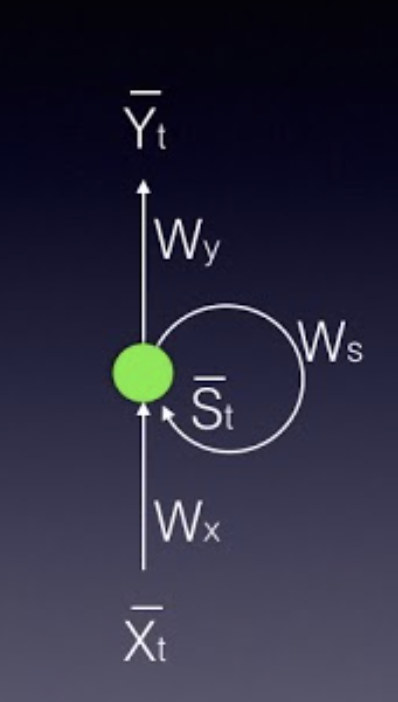
环神经网络的折叠模型
在这幅图中,\bar{x}表示输入向量,\bar{y} 表示输出向量,而\bar{s}表示状态向量。
W_x是连接输入层到状态层的权重矩阵。
W_y是连接状态层到输出层的权重矩阵。
W_s表示连接之前时间步长状态到当前时间步长状态的权重矩阵。
这个模型也可以是"基于时间的展开"。展开模型通常是我们处理循环神经网络时使用的方法。
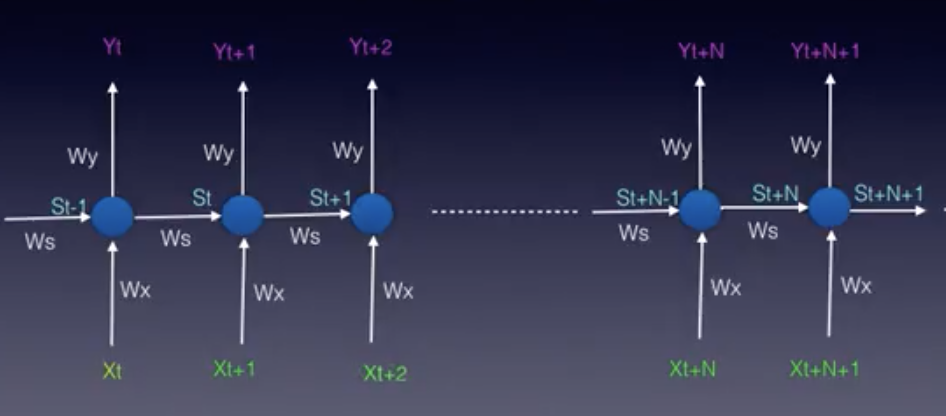
循环神经网络的展开模型
上述提到的折叠模型和展开模型中,均使用以下符号:
\bar{x}表示输入向量,\bar{y}表示输出向量,而\bar{s}表示状态向量。
W_x是连接输入到状态层的权重矩阵。
W_y是连接状态层到输出层的权重矩阵。
W_s表示连接之前时间步长状态到当前时间步长状态的权重矩阵。
在前馈神经网络中,隐藏层只取决于当前的输入和权重、以及激活函数\Phi,具体如下:
方程式 30
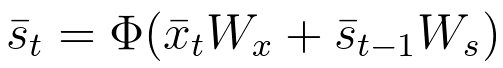
方程式31
输出向量的计算与前馈神经网络中完全一致。它是对应权重矩阵W_y的输入到每个输出节点的线性组合,也可以是相同线性组合的softmax函数。
或
\bar{y}_t=\sigma(\bar{s}_t W_y)
方程式 32
接下来的视频将侧重于展开模型,因为我们想进一步了解这个内容。